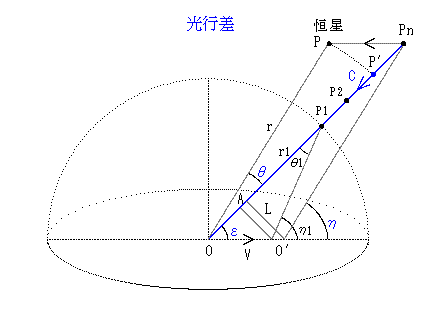
惷巭偟偰偄傞偲偒偺揰O偐傜偺峆惎偺埵抲傪P丄堏摦拞偺偲偒偺尒妡偗偺埵抲傪 P1, P2, 乧, P亴,Pn偲偡傞丅
P偺崅搙傪 兣[亱], Pn偺崅搙傪 兠[亱], 堏摦懍搙傪V, 岝懍搙傪C偲偡傞丅
岝攇偑懍搙C偱P-O娫傪堏摦偟偰偄傞偑丄兤 偺妏搙嵎偑偁傞傛偆偵尒偊傞丅
宱楬P-O偺婎弨嵗昗偵丄
憡懳懍搙岠壥偲偟偰偺尒妡偗偺宱楬Pn-O偺嵗昗傪廳偹偨嫟捠嵗昗偐傜丄V, 兤 偺娭學幃傪媮傔傞丅
宱楬Pn-O偵偍偄偰丄岝攇偑P1偐傜O偵岦偗偰懍搙C偱弌敪偟偨偲偡傞偲丄
OP1亖r1亖C嚈T1,丂OO亴亖V嚈T1,丂AO亴亖L1,
AP1亖r1亅V嚈T1cos兠,丂兠亖兾亅兤1亅(兾亅兣1)亖兣1亅兤1,丂tan兤1亖L1/AP1
L1亖(C嚈T1亅V嚈T1cos兠)亊tan兤1丂丂丂丂丂丂 嘆
L1亖V嚈T1亊sin兠丂丂丂丂丂丂丂丂丂丂丂丂丂丂嘇
嘆, 嘇傛傝丄Vsin兠亖(C亅Vcos兠)亊tan兤1丂丂 嘊
嘊偺椉曈偵cos兤1傪偐偗傞偲丄Vsin兠亊cos兤1亖(C亅Vcos兠)亊sin兤1
Vsin兠亊cos兤1亄Vcos兠亊sin兤1亖Csin兤1丂丂壛朄掕棟偵傛傝丄 Vsin(兠亄兤1)亖Csin兤1
丅
亪 sin兤1亖(V/C)亊sin(兠亄兤1)亖(V/C)亊sin兣1
摨條偵丄 sin兤2亖(V/C)亊sin兣2,丂乧,丂sin兤亴亖(V/C)亊sin兣亴丅
峆惎偺尒妡偗偺埵抲偑Pn偵偁傞傛偆偵尒偊傞偲偡傞偲丄
P-O娫偲Pn-O娫偺捠夁帪娫偼摨偠側偺偱丄宱楬Pn-O偺尒妡偗偺懍搙亖C亇嚈V 丅
宱楬Pn-O嵗昗偺帪娫傪憡懳帪娫偲偟丄宱楬Pn-O忋偺懍搙傪C偲偡傞偲丄
嫟捠嵗昗偵偍偗傞嫍棧偲妏搙偺娭學偐傜丄 sin兤n亖(V/C)亊sin兣n 丅
亪 sin兤亖(V/C)亊sin兣
忋恾偺偲偒丄尒妡偗偺崌惉懍搙(V_Pn-O, 憡懳懍搙)偑C傛傝懍偔側偭偰偄傞丅
憡懳帪娫偼丄C/V_Pn-O 攞偲側傞丅 [ 愙嬤帪娫偼丄V偺宱楬Pn-O曽岦惉暘偵娭偡傞帪娫姺嶼暘偑抁偔側傞丅]
( 懍搙傗帪娫偑榗傓傢偗偱偼側偔丄尒妡偗偺尰徾偲偟偰偺悢抣偲側傞丅)
( 峆惎偺尒妡偗偺埵抲Pn傗崅搙兠偼丄揰O偺嵗昗埲奜偱偼嫊悽奅偺傕偺偱偁傝丄
丂憡懳懍搙,憡懳帪娫偼丄揰O偺嵗昗忋偱偼幚悽奅偺傕偺丅)
佢P亖兾亅兤亅兠亖兾亅兤亅(兣亅兤)亖兾亅兣,丂Pn-O亖X,丂P-O亖r亖C嚈T,丂Pn-P亖V嚈T
X^2亖r^2亄(V嚈T)^2亅2rV嚈Tcos(兾亅兣)亖(C嚈T)^2亄(V嚈T)^2亄2CV嚈T^2cos兣
丂 亖嚈T^2(C^2亄V^2亄2CVcos兣)丂丂丂X亖嚈T併[C^2亄V^2亄2CVcos兣]
亪 V_Pn-O亖併[C^2亄V^2亄2CVcos兣]
( 宱楬Pn-O偺傛偆偵尒偊傞偑丄幚嵺偼宱楬P-O忋傪懍搙C偱岝攇偑摓払偟偰偄傞丅)
擭廃岝峴嵎 (懢梲)
V亖抧媴偺岞揮懍搙亖29.78亊10^3丂 C亖2.99792458亊10^8丂墿堒亖兝[亱]
丂懢梲偺兝佮0
[愒摴忋丆懢梲偺愒堒亖0丆惓拞帪]偺偲偒偺揤懱偺崅搙 兣亖90亅兝 丂亪 sin兤亖(V/C)亊cos兝
擭廃岝峴嵎 兤佮20.49[亶]丂丂( sin兤佮V/C )
( 杒敿媴偱偼懢梲偺惓拞帪亖撿拞帪 )
擭廃岝峴嵎偺敪尒丂僕僃乕儉僘丒僽儔僢僪儗乕(1728擭)丂James Bradley(1693亅1762)丂戞俁戙僌儕僯僢僕揤暥戜挿
帺戭偺揤捀僙僋僞乕偱峆惎偺懭墌塣摦偐傜敪尒丄傎偐偵1747擭偵復摦( 廃婜18.6擭丂掕悢9.2025亶)傪敪尒丅
( 塉悅偺拞傪堏摦偡傞偲偒偵尒偊傞塉偺摦偒偼丄堏摦偲媡岦偒偺懍搙偲塉偺棊壓懍搙偲偺儀僋僩儖崌惉偵傛傞傕偺丅)
[ 2009擭5寧, 12寧, 2011擭1寧 ]
俙俿俫俹僩僢僾儁乕僕