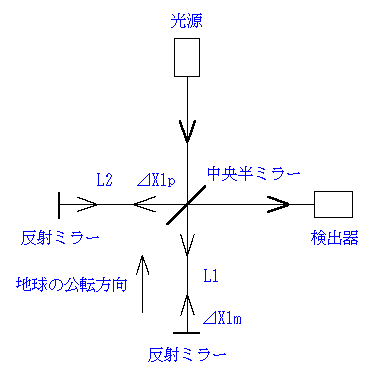
�}�C�P���\���]���[���[�̎���
�}�C�P���\���]���[���[�̎����ł́A
�n���̈ړ������ɕ��s�ƂȂ���̌o�H���������Ă��邽�߁A�o�H�����̌덷���]���u�ɂ��덷�̂��߁A
���g�̌��|��̑��x�ω������o�ł��Ȃ������Ǝv���B( �h�b�v���[���ʂɂ��g���̕ω����ŏ������ )
�n���̌��]���x��V, ���s�o�H��L1, ���p�o�H��L2, ���s�o�ߎ��Ԃ���T1, ���p�o�ߎ��Ԃ���T2,
L1��L2��L �Ƃ��āA�����n���ɑ��āA�s���ɋ߂Â����Ƃ���ƁA
���H�́A���g�̑��x��C�A���Α��x��C�{V�A������L�|��X1m�A(���˃~���[���߂Â�)
���H�́A���g�̑��x��C�A���Α��x��C�|V�A������L�{��X1p�B(�����~���[����������)
(L�{��X1p)/C����X1p/V�@(L�|��X1m)/C����X1m/V�@( C=2.99792458E8[m/s]�@V(�N����)��2.978E4[m/s] )
��T1��[L�|��X1m]/C�{[L�{��X1p]/C��2L/C�{[��X1p�|��X1m]/C
�@�@��2L/C�{L[V/(C�|V)�|V/(C�{V)]/C��L[2�{V/(C�|V)�|V/(C�{V)]/C
�@�@��L[2(C^2�|V^2)�{V(C�{V)�|V(C�|V)]/C(C^2�|V^2)��L[2C^2]/C(C^2�|V^2)
�@�@��2L/C�~C^2/(C^2�|V^2)��2L/C�~1/[1�|(V/C)^2]
�@�@��(2L/C)�~(1�{10^-8)�@�@(9.87�~10^-9)
L2�̌��g�͒n���̈ړ������ɑ��A���p�����ɓ`��邪�A���˃~���[�ւ̊p�x�̐��l�����Ȃ��A
�����g�U���Ă���A�ړ����Ă��锽�˃~���[�ɂ��`���̂ŁA���p���͒ʉ߂����Ƃ��āA
��T2��2��[(��X2/2)^2�{L^2]/C����X2/V�B�@4V^2[(��X2/2)^2�{L^2]/C��(C��X2)^2�@��X2^2��4(VL)^2/(C^2�|V^2)
��T2��2��[(VL)^2/(C^2�|V^2)�{L^2]/C��2L��[V^2/(C^2�|V^2)�{1]/C
�@�@��2L��[[C^2/(C^2�|V^2)]/C��2L/C��[1�|(V/C)^2]
�@�@��(2L/C)�~(1�{5�~10^-9)�@�@(4.93�~10^-9)
���̊g�U���Ȃ��A�܂����˃~���[������A��T2��2L/C (���p��)�B
( ���̔}���ׂ�����Ȃ̂�����A���g�͊����ɂ���Ď��ʂ̂��闱�q�̂悤�Ɏ߂ɂ͂Ȃ�Ȃ��B)
���p�������̂Ƃ�
��T����T1�|��T2��2L/C/[1�|(V/C)^2]�|2L/C��2L/C[1/[1�|(V/C)^2]�|1]��2L/C[(V/C)^2/(1�|(V/C)^2)]
�@ ��2L/C�~1/[(C/V)^2)�|1]��(2L/C)�~10^-8 [s]
( ��T����T1�|��T2��(2L/C)�~(1�{10^-8)�|2L/C��(2L/C)�~10^-8 [s] )
L2��L, L1��L�{��L �Ƃ���
V��0 �̂Ƃ� ��T����T1�|��T2��2(L�{��L)/C�|2L/C��2��L/C
V��3�~10^4 �̂Ƃ�
��T����T1�|��T2��2(L�{��L)(1�{10^-8)/C�|2L/C��2L(1�{10^-8)/C�{2��L(1�{10^-8)/C�|2L/C
�@ ��2L�~10^-8/C�{2��L(1�{10^-8)/C��2[L�~10^-8�{��L(1�{10^-8)]/C
�@ ��2[L�~10^-8�{��L]/C
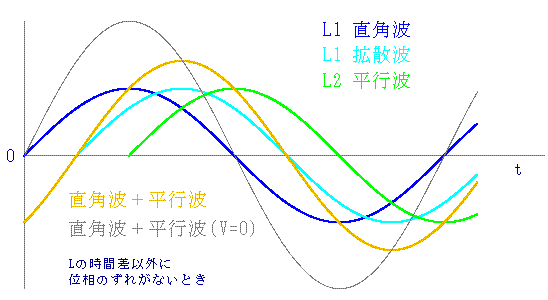
( V��0 �̂Ƃ��ɁA��L�ɂ��ʑ������v�����̔g���̐����{�ɂ���ɂ��A10L nm�ȉ��̒������x���K�v�B)
L��10m �̂Ƃ� ��T��6.67�~10^-16 [s]�@�g�̎����Ƃ���A
f��1.5�~10^15[Hz]�@�Ɂ�2�~10^-7[m]��200nm�B�@�v�����̔g����400nm�Ƃ���A1/2�g���B
|��L|��10^-7[m]�@100nm�ȉ��̐��x���K�v �B
( [��L��0, �����{]�ƂȂ�悤�ɁA6��,18�����ɒ������A��6���Ԍ�܂ŕω����Ȃ��悤�Ɉێ����Ȃ���Ȃ�Ȃ��B)
( �ܓx�Ӂ�0���̈ʒu���A���u���ӌX���Ă��Ȃ��ƁALsin�ӂɂ��e���Ő��m�ɒ����ł��Ȃ��B)
( ��]��������@�̂Ƃ����A�\��[��L��0, �����{]�̒������K�v�B)
�Œ���@�̂Ƃ��́A���Ȃ̕ω������Ԃ̌o�߂ƘA�����Ă���A���Α��x�ɂ��e���̗]�n������B
��]���@�̂Ƃ��́A��]�ɂ��덷�ŁA���Α��x�ɂ��e�����덷�ɖ�����邩������Ȃ��B
����̕��@�ł��A���B���Ԃ������g�U����L1���Ƃ̊��ȂƂȂ��āA���o�ł��Ȃ�������������Ȃ��B
�����~���[�����m��90���̔��˂ɂȂ�悤�ɁA�ǂ̂悤�ȕ��@�ōs�����̂��낤���A
�����A���ȂŒ������Ă����̂Ȃ�A�g�U���̂悤�Ɏ߂ɂȂ��Ă�����������Ȃ��B
( ���[�ł̒�������L��0 �łȂ������{�̂Ƃ��ƁA���������[�łȂ��Ƃ��B)
���m��[ �����~���[�̔��˂�90��, ��L��0 ]�� 90����]�������Ƃ��A���o��ɂ��������ʒu��
�����~���[�̓��ߌ��̈ʒu�𒆐S�ɉ�]�O��̔��ˌ��̈ʒu���Ώ̂ɂȂ�A
���ߌ��Ɣ��ˌ��̓��B�̎��ԍ��������Ȃ̂ŁA�������ȂɂȂ�Ǝv���B
[ �{��T(���ˌ�)��0(���ߌ�), 0(���ߌ�)�Ɓ|��T(���ˌ�) ]
( 90����]�O��̊��Ȃ̈ʒu�̍��͖�20pm�B[ L��10, V��3�~10^4 ] )
( ��]�̓r���͓����ɂȂ�Ȃ��B)
L1��L2�Ƃ̍��́A���x���������L1����L2���̌��o��ɂ��������ʒu�̍���������B
( ���x�����Ȃ��̂Ȃ�A�}�̂�}�̂ւ̍�p���n���ɑ�������Ă���̂�������Ȃ��B)
( �n���̎��]�ɂ��T�j���b�N���ʂ��m�F����Ă���̂�����A���x��������͂��B)
�����������ɁA���s�o�H, ���p�o�H ���ꂼ���������Ĉʑ����𑪒肷��悢��������Ȃ��B
��T1��[L�{��L�{��X1p]/C��[L�{��L�{LV/(C�|V)]/C��L/C�{[��L�{LV/(C�|V)]/C
���̊g�U�͂Ȃ��Ƃ��āA��T2��L/C�B �@��T����T1�|��T2��[��L�{LV/(C�|V)]/C
V/(C�|V)��9.93�~10^-5�@ ����T��[L�~10^-4�{��L]/C�@ ( �o�H�̋��e�덷�͉����̖�1���{ )
C��T����L�{LV/(C�|V)�@ (C��T�|��L)(C�|V)��LV�@ (C��T�|��L)C�|V(C��T�|��L)��LV
LV�{V(C��T�|��L)��(C��T�|��L)C�@ �@��V��(C��T�|��L)C/(C��T�{L�|��L)
��L��0 �̂Ƃ��AV��C^2/(C�{L/��T)�B
( ���]�ɂ�鑬�x(��465.2[m/s])�́AV�̋ߎ��l�����o�ł���悢�̂ŏȗ��B)
( ���z�𒆐S�Ƃ������W�Ō�����̂ŁA��͉�]���x(200�`240K[m/s])�͏��O�B)
( ��͒��S�� ��=17h45.6m �Ȃ̂ŁA�����͏t��,�H���̑O�オ�悢��������Ȃ��B)
���������Ȃ����@�Ō��]�ɂ�鑬�x�������o�ł��Ȃ���A�n���̊j�𒆐S�Ƃ������W�ŁA
���]�ɂ�鑬�x���������Ȃ���Ȃ�Ȃ���������Ȃ��B
( ���L���͂̌����ƂȂ��Ă��鍂�����q(����)�̑��z�ɂ��e���̔z�����K�v��������Ȃ��B)
MM�����Ƃ͈قȂ邪�A���t�@�C�o�[�œ��������̋����k�̒������n�_�Ƃ��A��������L/2, ��������L/2�̌o�H�����A
�������烌�[�U�[���A2�_(��,��)�ł̑��肩�玞�ԍ������߂�悢��������Ȃ��B
( ���v�k�ɂ�鎞�ԍ������̔}���ɑ��鑕�u�̓��������̈ړ��̉e���ƂȂ�B)
[ 2009�N5�� 2010�N1��,8��,9�� ]
�O�̃y�[�W�`�s�g�o�g�b�v�y�[�W
(�T�C�G���X��ʂɑ��鎄��,����)